可約表現の簡約で既約表現を得る？
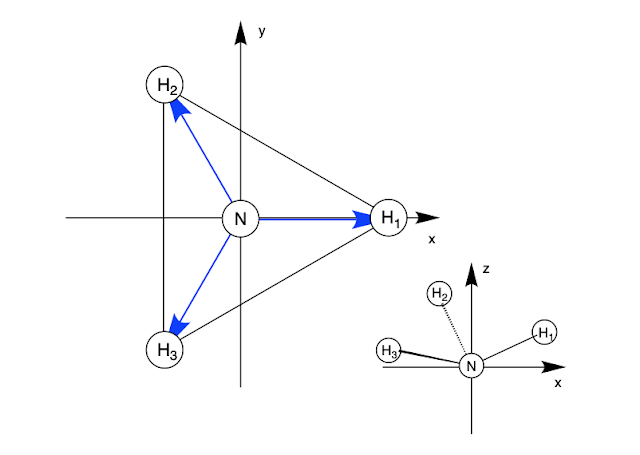
線形代数ネタですが、群論関係でのつまづいたところを共有したいと思います。 [導入] 分子軌道や、分子の振動モードについて理解しようと思うと、「群論」についての理解が必要です。電子遷移スペクトル（UV–vis）を始めとする各種分光で利用する許容や禁制も、対称性の議論が重要なので、避けて通れないトピックスです。みんな大好き（?）な、芳香族性について考えるときも、群論は顔をのぞかせます。さらには、ペリ環状反応が同旋的に進行するか逆旋的に進行するか、なんてことを考える際にもちらっと出てきますね。 私はここで出てくる「 可約表現 」を「 簡約 」して「 既約表現 」にする、というところがスッキリせず苦しみました。 この記事では、アンモニア分子のC3軸周りの回転操作を例に取って話を進めていきますが、この操作を記述する方法はたくさんあります。 水素原子の座標を決めてやり、回転行列と呼ばれる行列を掛けてやることでも回転を表現できます。また、そんなカッコいいものを使わなくても、{ H(水素)1をH2の位置に、H2をH3の位置に、H3をH1の位置にまとめて移動} = C3回転 という操作は、以下のように示してやることもできます。 \begin{align}\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix} \begin{pmatrix} H_{1}\\ H_{2}\\ H_{3}\end{pmatrix} =\begin{pmatrix} H_{2}\\ H_{3}\\ H_{1}\end{pmatrix} \end{align} 複素数を掛けることも回転操作に対応している、というのもどこかで聞いたことがあると思います。 このように見ると、なんでおんなじ事するのに色々あるんだよ！とモヤモヤする方もいると思いますが、逆に考えると、これらの操作に共通する性質があるんちゃう？と見るのが群論です。 （この辺りをサラッと知りたい人はヨビノリの動画もいいですよ。） 同じ操作をするのであれば、一番使いやすい形にしようぜ！ってゆうモチベーションが出てきますよね？上に1と0で書いた操作は、正三角形の頂点に置かれた点の組（つまり点群ですね）を考えたから成立するわけで、