可約表現の簡約で既約表現を得る?
線形代数ネタですが、群論関係でのつまづいたところを共有したいと思います。
[導入] 分子軌道や、分子の振動モードについて理解しようと思うと、「群論」についての理解が必要です。電子遷移スペクトル(UV–vis)を始めとする各種分光で利用する許容や禁制も、対称性の議論が重要なので、避けて通れないトピックスです。みんな大好き(?)な、芳香族性について考えるときも、群論は顔をのぞかせます。さらには、ペリ環状反応が同旋的に進行するか逆旋的に進行するか、なんてことを考える際にもちらっと出てきますね。
私はここで出てくる「可約表現」を「簡約」して「既約表現」にする、というところがスッキリせず苦しみました。
この記事では、アンモニア分子のC3軸周りの回転操作を例に取って話を進めていきますが、この操作を記述する方法はたくさんあります。
\begin{align} \mathbb{A} =\begin{pmatrix} \overrightarrow{H}_{1} \\ \overrightarrow{H}_{2}\\ \overrightarrow{H}_{3}\end{pmatrix} \end{align}
さらにこれを回転させましょう。3回軸に沿って水素をぐるりと回して出来るアンモニアをA'とすると、以下のような関係式で表現することができます。(上に示した例と同じですね。)
\begin{align} \begin{aligned}\mathbb{A'} =\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}\begin{pmatrix} \overrightarrow{H}_{1}\\ \overrightarrow{H}_{2}\\ \overrightarrow{H}_{3}\end{pmatrix} =\begin{pmatrix} \overrightarrow{H}_{2}\\ \overrightarrow{H}_{3}\\ \overrightarrow{H}_{1}\end{pmatrix}\end{aligned} \end{align}
ここで出てくる0と1でできた3×3行列が、回転についての表現です。C3と名付けます。少しくどいですが、これを使って関係を整理すると以下の式を得ます。
\begin{align} \mathbb{C}_{3} = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix} \end{align}
\begin{align} \mathbb{A'}=\mathbb{C}_{3}\mathbb{A} \end{align}
この行列の代わりに、単位行列を掛けると「その場から動かさない」という操作(恒等操作)になることが想像できますか?これはEと名付けられることが普通です。
\begin{align} \mathbb{E} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{align}
このように、位置の入れ替えは、0と1だけで簡単に表現することができます。
さて、C3v点群上のベクトルの組は、安心して(?)シンプルな0と1の行列で移動できるわけことを確認しました。
\begin{align} \overrightarrow {x} =\overrightarrow {H}_{1}-\dfrac {1}{2}\overrightarrow {H}_{2}-\dfrac {1}{2}\overrightarrow {H}_{3} \end{align}
H2 と H3 を半分ずつ入れてやることで、Y成分とZ成分がきれいに消えることを確認しましょう。
\begin{align} \overrightarrow {y}=-\dfrac {1}{\sqrt {2}}\overrightarrow{H}_{2}+\dfrac {1}{\sqrt {2}}\overrightarrow{H}_{3} \end{align} \begin{align} \overrightarrow {z}=\dfrac {1}{\sqrt {3}}\overrightarrow{H}_{1}+\dfrac {1}{\sqrt {3}}\overrightarrow{H}_{2}+\dfrac {1}{\sqrt {2}}\overrightarrow{H}_{3} \end{align}
これらをまとめると、デカルト座標系を表すベクトルの組 X は、ベクトルの組 A に、行列を掛けた形式で書けることがわかります。また、この座標系を変換する機能を持った行列をTとしておきます。
これを上手くつかいます。
A'をTで座標変換すればX'になるはずです。また、A' = CA の関係がありました。
\begin{align} \mathbb{X'}=\mathbb{T}\mathbb{C}_{3}\mathbb{T}^{-1}\mathbb{X} \end{align}
C3をT(-1)とTで挟んでいるところを、ひとかたまりと見ましょう(大事)。
この塊は、Xを120°回転させてX'へと変換する操作を表しています。
\begin{align} \mathbb{T}\mathbb{C}_{3}\mathbb{T}^{-1} = \left( \begin{array}{cc|c} -\dfrac {1}{2} & -\dfrac {\sqrt {3}}{2} & 0\\ \dfrac {\sqrt {3}}{2} & -\dfrac {1}{2} & 0\\ \hline 0 & 0 & 1\\ \end{array} \right) = \left( \begin{array}{cc|c} \cos{120°} & -\sin{120°} & 0\\ \sin{120°} & \cos{120°} & 0\\ \hline 0 & 0 & 1\\ \end{array} \right) = \mathbb{R}_{3} \end{align}
逆行列を掛けるこれら一連の式変形は、物理化学を学ぶ上で頻出です。
(数3Cで、逆行列を左からかけて、行列を右からかける計算をさせられた記憶がかすかに脳裏をかすめますね。)
ここで利用した直交行列ですが、複素数まで適用範囲を拡張したものが、エルミート行列と呼ばれます。
(前に、行列の種類について書きました。実際にどんな感じで利用するのかについてはEMANさんのページがわかりやすいです。)
[まとめ] 行列がブロックに分けられたことが今回の最大のポイントです。この行列Rは、左上の成分と右下の成分(ここでは1だけです)で、示すことができます。このように、変換操作を一般的な形に落とし込んで、より小さなブロック行列(ガンマ:Γ)に分割していくことを簡約といいます。RはΓ(3)とΓ(1)の「直和」で表現できます(ようやく終着点です。)
\begin{align} \mathbb{R} = \Gamma _{3}+\Gamma _{1}\\ \end{align}
\begin{align} (\Gamma _{3} = \begin{pmatrix} cos{120°} & –sin{120°} \\sin{120°} & cos{120°}\end{pmatrix}, \quad \Gamma _{1} =\begin{pmatrix}1\end{pmatrix}) \end{align}
この、Γ(1)とΓ(3)は、化学の教科書ではA(1)、Eと書かれているものです。マリケンが名前をつけたことから、マリケン表記と呼ばれます。
この簡約操作は、C(3)以外にも、面対称な移動などの他の対称操作についても、全く同じように議論することができます。 ここではそのすべてを示しませんが、AISTの吉澤先生の資料や、新潟大佐藤先生の資料、名古屋工業大川崎先生の資料を参照していただけると、全体がつかめるかと思います。
簡約された行列の対角成分(いわゆるtrace)は、線形代数的に深淵な意味(すみません、スッキリ表現できないだけです)を持っていて、操作の特徴を決定づけます。
これをまとめたものが、指標表と呼ばれるもので、教科書の後ろの方にあるのを見たことがある人も多いはずです。 これを利用すると、分子についての情報をこれでもかというほど引き出すことが出来るのですが、その内容は群論の教科書を参照すると良いでしょう。
あれ、Γ(1)とΓ(3)、が出てきて、Γ(2)は?と、思った方もいるかも知れません。
C3v群の指標表を見ると、A(2)と書かれているものがありますが、これがΓ(2)に対応します。
[導入] 分子軌道や、分子の振動モードについて理解しようと思うと、「群論」についての理解が必要です。電子遷移スペクトル(UV–vis)を始めとする各種分光で利用する許容や禁制も、対称性の議論が重要なので、避けて通れないトピックスです。みんな大好き(?)な、芳香族性について考えるときも、群論は顔をのぞかせます。さらには、ペリ環状反応が同旋的に進行するか逆旋的に進行するか、なんてことを考える際にもちらっと出てきますね。
私はここで出てくる「可約表現」を「簡約」して「既約表現」にする、というところがスッキリせず苦しみました。
この記事では、アンモニア分子のC3軸周りの回転操作を例に取って話を進めていきますが、この操作を記述する方法はたくさんあります。
水素原子の座標を決めてやり、回転行列と呼ばれる行列を掛けてやることでも回転を表現できます。また、そんなカッコいいものを使わなくても、{ H(水素)1をH2の位置に、H2をH3の位置に、H3をH1の位置にまとめて移動} = C3回転 という操作は、以下のように示してやることもできます。
\begin{align}\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix} \begin{pmatrix} H_{1}\\ H_{2}\\ H_{3}\end{pmatrix} =\begin{pmatrix} H_{2}\\ H_{3}\\ H_{1}\end{pmatrix} \end{align}
複素数を掛けることも回転操作に対応している、というのもどこかで聞いたことがあると思います。
このように見ると、なんでおんなじ事するのに色々あるんだよ!とモヤモヤする方もいると思いますが、逆に考えると、これらの操作に共通する性質があるんちゃう?と見るのが群論です。(この辺りをサラッと知りたい人はヨビノリの動画もいいですよ。)
同じ操作をするのであれば、一番使いやすい形にしようぜ!ってゆうモチベーションが出てきますよね?上に1と0で書いた操作は、正三角形の頂点に置かれた点の組(つまり点群ですね)を考えたから成立するわけで、この行列をそのへんの適当な点に掛けても、もちろん軸回りの120°回転にはなりません。
一般的な座標系に対して使える、適当な回転操作(の可約表現)をみつけて、それをできるだけ一般的な形に書き換え(簡約)、それ以上シンプルなものはない、という形(既約表現)にしてみましょう。
簡約とは、行列を、等価でよりシンプルな扱いやすい形へと変換する操作です。
[本文] では、アンモニアの水素原子のC3回転を出発点として、C3回転の既約表現を探してみましょう。
1) 回転操作を表現する行列をつくる(C3v対称の系での表現)
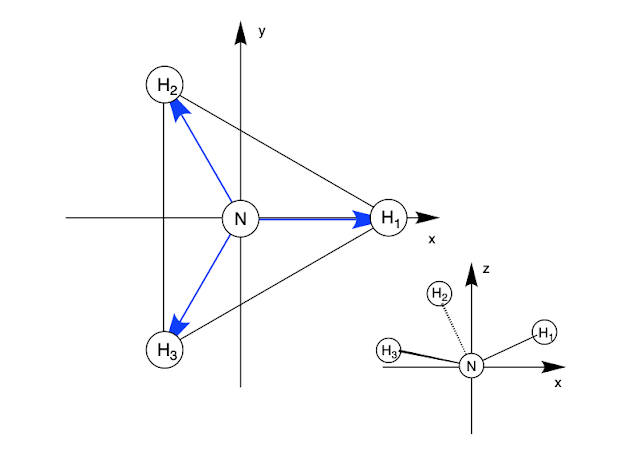
窒素の位置を原点として、座標系は以下のように取ります。都合により、水素は窒素からみて上に置きました。

窒素の位置を原点ベクトルOとして、3つの水素原子へと伸びるベクトルをそれぞれH1, H2, H3と命名します。このとき、この図のような3つの水素の配置は、下のようなベクトルの組Aで表わされます。
\begin{align} \mathbb{A} =\begin{pmatrix} \overrightarrow{H}_{1} \\ \overrightarrow{H}_{2}\\ \overrightarrow{H}_{3}\end{pmatrix} \end{align}
さらにこれを回転させましょう。3回軸に沿って水素をぐるりと回して出来るアンモニアをA'とすると、以下のような関係式で表現することができます。(上に示した例と同じですね。)
\begin{align} \begin{aligned}\mathbb{A'} =\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}\begin{pmatrix} \overrightarrow{H}_{1}\\ \overrightarrow{H}_{2}\\ \overrightarrow{H}_{3}\end{pmatrix} =\begin{pmatrix} \overrightarrow{H}_{2}\\ \overrightarrow{H}_{3}\\ \overrightarrow{H}_{1}\end{pmatrix}\end{aligned} \end{align}
ここで出てくる0と1でできた3×3行列が、回転についての表現です。C3と名付けます。少しくどいですが、これを使って関係を整理すると以下の式を得ます。
\begin{align} \mathbb{C}_{3} = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix} \end{align}
\begin{align} \mathbb{A'}=\mathbb{C}_{3}\mathbb{A} \end{align}
この行列の代わりに、単位行列を掛けると「その場から動かさない」という操作(恒等操作)になることが想像できますか?これはEと名付けられることが普通です。
\begin{align} \mathbb{E} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{align}
このように、位置の入れ替えは、0と1だけで簡単に表現することができます。
逆回転を示す行列C3'や、NとH1を通る鏡面を使った対称移動なんかも同様です。
さて、C3v点群上のベクトルの組は、安心して(?)シンプルな0と1の行列で移動できるわけことを確認しました。
2) 一般的な座標系で通用する回転操作の表現をみつける (可約表現の一つを見つける)
続いて、デカルト座標系を考えて、その上にある任意の点を120°回転移動させられる行列はどんなものでしょうか。それをみつける戦略は以下の通り。
戦略__________
より一般的なx, y, z の直交座標系のベクトルを、さきほど作ったH1, H2, H3ベクトルで表現してみます。一見遠回りですが、この操作を通じてC3v対称系における表現とデカルト座標系における表現の橋渡しをするきっかけを掴みます。
この操作から、座標系を変換するための行列を作ることができます。
一度このような変換行列を作ることができれば、その逆の操作について考えることもできるようになります!
この座標系を変換する行列を上手くつかえば、さっき作った0と1だけの回転行列を、より一般的な表現に変換できるんじゃね?と考えます。
____________
それでは x を H1, H2, H3 で表現してみます。
x = H1 と、シンプルに行けそうなものですが、H1はz成分を持っています。
これをきれいに打ち消してやるには、H2 と H3 の力添えが必要です。
\begin{align} \overrightarrow {x} =\overrightarrow {H}_{1}-\dfrac {1}{2}\overrightarrow {H}_{2}-\dfrac {1}{2}\overrightarrow {H}_{3} \end{align}
H2 と H3 を半分ずつ入れてやることで、Y成分とZ成分がきれいに消えることを確認しましょう。
続いて、| x | = 1 としたいので、このベクトルの大きさを調節(規格化)します。
具体的には、それぞれの係数を二乗して足したら1に成るように係数を決定します。
\begin{align} \overrightarrow {x}=\dfrac {2}{\sqrt {6}}\overrightarrow{H}_{1}-\dfrac {1}{\sqrt {6}}\overrightarrow{H}_{2}-\dfrac {1}{\sqrt {6}}\overrightarrow{H}_{3} \end{align}
つづいて y です。H1はXZ平面上にあることから、y は H1 とは直交関係にあります。
\begin{align} \overrightarrow {x}=\dfrac {2}{\sqrt {6}}\overrightarrow{H}_{1}-\dfrac {1}{\sqrt {6}}\overrightarrow{H}_{2}-\dfrac {1}{\sqrt {6}}\overrightarrow{H}_{3} \end{align}
つづいて y です。H1はXZ平面上にあることから、y は H1 とは直交関係にあります。
つまり y は、H2とH3だけで表現できます。
また z は、H1、H2、H3 がそれぞれ持っているX成分とY成分が消えるように足し合わせることで作ることができます。規格化まで行うと、
\begin{align} \overrightarrow {y}=-\dfrac {1}{\sqrt {2}}\overrightarrow{H}_{2}+\dfrac {1}{\sqrt {2}}\overrightarrow{H}_{3} \end{align} \begin{align} \overrightarrow {z}=\dfrac {1}{\sqrt {3}}\overrightarrow{H}_{1}+\dfrac {1}{\sqrt {3}}\overrightarrow{H}_{2}+\dfrac {1}{\sqrt {2}}\overrightarrow{H}_{3} \end{align}
これらをまとめると、デカルト座標系を表すベクトルの組 X は、ベクトルの組 A に、行列を掛けた形式で書けることがわかります。また、この座標系を変換する機能を持った行列をTとしておきます。
\begin{align} \mathbb{X}=\begin{pmatrix} \overrightarrow {x} \\ \overrightarrow {y} \\ \overrightarrow {z} \end{pmatrix} =\begin{pmatrix} \dfrac {2}{\sqrt {6}}& \dfrac {1}{\sqrt {6}} & -\dfrac {1}{\sqrt {6}} \\ 0&-\dfrac {1}{\sqrt {2}} & \dfrac {1}{\sqrt {2}} \\ \dfrac {1}{\sqrt {3}}&\dfrac {1}{\sqrt {3}} & \dfrac {1}{\sqrt {3}} \end{pmatrix} \begin{pmatrix} {\overrightarrow{H}_{1}} \\ \overrightarrow{H}_{2}\\ \overrightarrow{H}_{3} \end{pmatrix} =\mathbb{T}\mathbb{A} \end{align}
\begin{align} \mathbb{T}= \begin{pmatrix} \dfrac {2}{\sqrt {6}}& \dfrac {1}{\sqrt {6}} & -\dfrac {1}{\sqrt {6}} \\ 0&-\dfrac {1}{\sqrt {2}} & \dfrac {1}{\sqrt {2}} \\ \dfrac {1}{\sqrt {3}}&\dfrac {1}{\sqrt {3}} & \dfrac {1}{\sqrt {3}} \end{pmatrix} \end{align}
___________
少し脇道です。
当たり前ですがデカルト座標を作るx, y, z ベクトルはそれぞれ直交しているはずです。
x と y の式(8と9)の内積がゼロであることを確認してみましょう。
一行と二行の内積は以下の通り。
\begin{align} \overrightarrow {x} \cdot \overrightarrow {y} = \dfrac{2}{\sqrt{6}}\times 0+\left( -\dfrac{1}{\sqrt{6}}\right)\times\left(-\dfrac{1}{\sqrt{2}}\right)+\left( -\dfrac{1}{\sqrt{6}}\right)\times\dfrac{1}{\sqrt{2}}= 0 \end{align}
もちろん二行と三行、一行と三行の内積も0になります。係数の2乗の和は1になるように決めました。つまり、Tの行はそれぞれ直行するベクトルを表現しています。
このような性質を持った行列を「直交行列」と呼びます。
列についても見てやりましょう。それぞれの列をベクトルに分割してみてやると、それぞれの内積がゼロになっていること、また列ベクトルの大きさが0になることを確認できるでしょうか?
かなりごちゃごちゃとしているように見えますが、このTはかなりキレイな素性を持っていそうなことが分かるかと思います。
___________
このTは、前の記事にも書いた「合同変換」を行う行列です。
[ 前の記事:回転行列(なんでマイナスが右上に?)]
この合同変換を行う行列は必ず直行行列となります。それがなんだってゆうのか?
直交行列は転置をしてやると逆行列になります。逆行列を作るのって、結構面倒なんですよね。
嘘だと思うなら、それぞれを掛けるとEが得られることを確かめて見ましょう。
\begin{align}
\mathbb{T}^{-1} = \mathbb{T}^{t} =
\begin{pmatrix}
\dfrac {2}{\sqrt {6}} & 0 & \dfrac {1}{\sqrt {3}}
\\ \dfrac {1}{\sqrt {6}} & -\dfrac {1}{\sqrt {2}} & \dfrac {1}{\sqrt {3}}
\\ -\dfrac {1}{\sqrt {6}} & \dfrac {1}{\sqrt {2}} & \dfrac {1}{\sqrt {3}} \end{pmatrix}
\end{align}
\begin{align} \mathbb{T}^{-1}\mathbb{T} =\mathbb{E} \end{align}
これを使うと、(11)式から以下のような関係が得られます。
\begin{align} \mathbb{T}^{-1}\mathbb{T} =\mathbb{E} \end{align}
これを使うと、(11)式から以下のような関係が得られます。
\begin{align} \mathbb{T}^{-1}\mathbb{X} =\mathbb{T}^{-1}\mathbb{T}\mathbb{A} \end{align}
\begin{align} \mathbb{T}^{-1}\mathbb{X} =\mathbb{A} \end{align}
つまり、Aの座標系で表現された座標系にTを掛けることでXの座標系(デカルト)へ、
Xの座標系(デカルト)に、T-1を掛けることでAの座標系で表現された座標系へと変換できます。
これを上手くつかいます。
「Aの座標系で表現されたベクトルを、C3で120°回転させてA'を得る」
この一連の操作を変換して、
「Xの座標系で表現されたベクトルを、120º回転させてX'を得る」
にはどうすればよいでしょうか。
これは以下の式のようになります。
\begin{align} \mathbb{X'}=\mathbb{T}\mathbb{A'} =\mathbb{T}\mathbb{C}_{3}\mathbb{A} \end{align}
さらに17式をつかうことで、この式からAを消すことができます。
\begin{align} \mathbb{X'}=\mathbb{T}\mathbb{A'} =\mathbb{T}\mathbb{C}_{3}\mathbb{A} \end{align}
さらに17式をつかうことで、この式からAを消すことができます。
\begin{align} \mathbb{X'}=\mathbb{T}\mathbb{C}_{3}\mathbb{T}^{-1}\mathbb{X} \end{align}
C3をT(-1)とTで挟んでいるところを、ひとかたまりと見ましょう(大事)。
この塊は、Xを120°回転させてX'へと変換する操作を表しています。
この行列3連発を真面目に計算して、まとめたものを行列R3と置きます。
ルートの6が消えて、見慣れた数字が並びます。
これはsinとcosでさらにきれいにまとめることができます。
\begin{align} \mathbb{T}\mathbb{C}_{3}\mathbb{T}^{-1} = \left( \begin{array}{cc|c} -\dfrac {1}{2} & -\dfrac {\sqrt {3}}{2} & 0\\ \dfrac {\sqrt {3}}{2} & -\dfrac {1}{2} & 0\\ \hline 0 & 0 & 1\\ \end{array} \right) = \left( \begin{array}{cc|c} \cos{120°} & -\sin{120°} & 0\\ \sin{120°} & \cos{120°} & 0\\ \hline 0 & 0 & 1\\ \end{array} \right) = \mathbb{R}_{3} \end{align}
これは、、、(ゴクリ)。左上のブロックは、前に書いた回転行列にほかなりません。右下の1が加わり3×3行列になると、z軸は固定してxy平面に並行に点を回す操作の一般系となります。
初めの回転操作を表す行列C3は、対角上に0がない行列でしたが、新たに得られたR3はブロック対角化(できるところまでは対角化したようなもの)になっています。
このように、可約な回転の表現をできるだけ対角化していくことにより既約な表現が得られます。この操作を簡約というわけです。
なぜ、対角化したいのかって?それは実際に計算を行う場合の計算量が劇的に減らせるからです。
逆行列を掛けるこれら一連の式変形は、物理化学を学ぶ上で頻出です。
(数3Cで、逆行列を左からかけて、行列を右からかける計算をさせられた記憶がかすかに脳裏をかすめますね。)
ここで利用した直交行列ですが、複素数まで適用範囲を拡張したものが、エルミート行列と呼ばれます。
(前に、行列の種類について書きました。実際にどんな感じで利用するのかについてはEMANさんのページがわかりやすいです。)
[まとめ] 行列がブロックに分けられたことが今回の最大のポイントです。この行列Rは、左上の成分と右下の成分(ここでは1だけです)で、示すことができます。このように、変換操作を一般的な形に落とし込んで、より小さなブロック行列(ガンマ:Γ)に分割していくことを簡約といいます。RはΓ(3)とΓ(1)の「直和」で表現できます(ようやく終着点です。)
\begin{align} \mathbb{R} = \Gamma _{3}+\Gamma _{1}\\ \end{align}
\begin{align} (\Gamma _{3} = \begin{pmatrix} cos{120°} & –sin{120°} \\sin{120°} & cos{120°}\end{pmatrix}, \quad \Gamma _{1} =\begin{pmatrix}1\end{pmatrix}) \end{align}
この、Γ(1)とΓ(3)は、化学の教科書ではA(1)、Eと書かれているものです。マリケンが名前をつけたことから、マリケン表記と呼ばれます。
今回取り扱ったz軸の周りの回転では、Z座標の値は変化しません。つまり考えなくてもいいわけです。一方で、X座標とY座標は、お互いが混ざり合いながら干渉し合いながら変化します。つまり、不可分なわけです。
これ以上、2×2行列であるΓ(3)が分割できないのは、これを意味しているわけです。
この簡約操作は、C(3)以外にも、面対称な移動などの他の対称操作についても、全く同じように議論することができます。 ここではそのすべてを示しませんが、AISTの吉澤先生の資料や、新潟大佐藤先生の資料、名古屋工業大川崎先生の資料を参照していただけると、全体がつかめるかと思います。
簡約された行列の対角成分(いわゆるtrace)は、線形代数的に深淵な意味(すみません、スッキリ表現できないだけです)を持っていて、操作の特徴を決定づけます。
これをまとめたものが、指標表と呼ばれるもので、教科書の後ろの方にあるのを見たことがある人も多いはずです。 これを利用すると、分子についての情報をこれでもかというほど引き出すことが出来るのですが、その内容は群論の教科書を参照すると良いでしょう。
あれ、Γ(1)とΓ(3)、が出てきて、Γ(2)は?と、思った方もいるかも知れません。
C3v群の指標表を見ると、A(2)と書かれているものがありますが、これがΓ(2)に対応します。
(2020/3/2改訂 単位行列E の記載など、誤植を直しました。混乱してしまった方がいたら申し訳有りません。)
(2020/3/6改訂 導入部分を少し加筆)
(2020/8/29改訂 大幅改訂 C3の表現、Eの表現に誤植がありました。直したとおもっていたのですが、、半年間いろいろと物理、数学をやったおかげでだいぶ見通しがよい記事になってきたのでは。)
(2020/3/6改訂 導入部分を少し加筆)
(2020/8/29改訂 大幅改訂 C3の表現、Eの表現に誤植がありました。直したとおもっていたのですが、、半年間いろいろと物理、数学をやったおかげでだいぶ見通しがよい記事になってきたのでは。)

コメント
コメントを投稿