分子軌道の表示 [isovalueってなに？]

分子の軌道は、計算によって得られる重要な情報の一つです。細かな話ですが、その記述の際のポイントに付いてです。

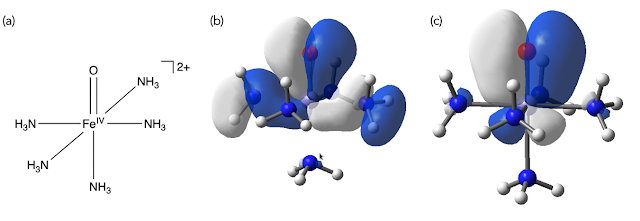
トップの画像の左右は、同じ錯体分子（[Fe(O)(NH3)5]2+, 水素は表示していません）の軌道の一つです。違うのは、黄色い点線で示した「isovalue」という数値の大きさです。

ご存知のように、電子は原子核の近くにより大きな存在確率を持っており、原子核から離れるほどその存在確率は小さくなります。一つの分子軌道にはアップスピン、ダウンスピンの電子が１つづつ入りますが、その存在確率は、無限遠まで足し合わせることで２になります。

軌道を描画する際には、無限遠まで表示してもなんのこっちゃわかりませんので、適当なところで区切る必要があります。その設定が「isovalue」の値となります。

単位は、1(e-)/1Å^3 となります。これは、1Å角の立方体に、1電子入っているときの値を1とする単位系です。

（文献を読む場合には、体積の単位系に、Å の代わりに原子単位系のBorh [≒0.53 Å] を利用しているケースもあるようなので、注意してください。）

上の例では、左は0.02 (e-)/Å^3 の密度になるところまで表記しています。表面の内側の電子密度は 0.02 (e-)/Å^3 より大きくなっています。右の例では0.1 (e-)/Å^3 の密度になるところまで軌道を表示しています。どちらも、もちろん間違いではありませんが、電子密度のより高いところだけを表記したほうが、その軌道に「主に」寄与する軌道がハッキリする点でおすすめです（何をディスカッションしたいかによりますね）。

上の例は、鉄のオキシド錯体のHOMOを表示しています。配位子場理論では、金属錯体のHOMO近傍の軌道は中心金属のd軌道と、配位子の軌道の反結合性軌道で近似されますが、右の例ではその様子が見られます。一方、左の例では、一つの軌道に様々な原子軌道の寄与が実際にはあることがわかります。