回転行列(なんでマイナスが右上に?)
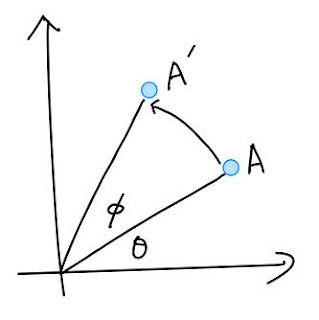
\begin{eqnarray} \boldsymbol{ R }=\begin{pmatrix} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{pmatrix} \end{eqnarray} 線形代数を触っていると出てくる回転行列 R 、分かったようでわからない。 スペクトルを理解したい→群論を理解したい→線形代数を身につける必要がある のような流れで、かならずぶつかると思います。 (当たり前だろって? 線形代数をきちんと勉強したあなたはエラい!) アホみたいな話ですが、非対称にマイナスが右上に出てくる理由について なかなか腹落ちできません。 左回り90°、ぐるりと点を動かすとcos (θ+π/2) = –sin θ , sin (θ+π/2) = cos θ で、非対称にマイナス記号が付くことなんかも、この問題と関係している。 (図形を描けば自明でも、不思議ではありませんか?これも昔から気持ち悪かった。) 暗記できても、なんだか気持ち悪いのはよくありません。 しばし思案して、スッキリとしたので備忘録です。 加法定理を使うとスッキリ理解できます。 ❏ 下の図で、単位円上にある点AをA'へと回転させるとしましょう。 A'の座標は、加法定理を使うと以下のように書けます。 (加法定理の図形的理解は、 こちらの図 が分かりやすい) \begin{eqnarray} A' = \begin{pmatrix}\cos(\theta+\phi)\\ \sin(\theta+\phi)\end{pmatrix} \end{eqnarray} 加法定理より、 \begin{eqnarray} \cos(\theta+\phi) =\cos\theta\cos\phi–\sin\theta\sin\phi =\begin{pmatrix}\cos\phi&-\sin\phi\end{pmatrix}\begin{pmatrix}\cos\theta \\ \sin\theta \end{pmatrix} \end{eqnarray} \begin{eqnarray} \sin(\theta+\p...
