回転行列(なんでマイナスが右上に?)
\begin{eqnarray}
\boldsymbol{ R }=\begin{pmatrix} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{pmatrix}
\end{eqnarray}
線形代数を触っていると出てくる回転行列R、分かったようでわからない。
スペクトルを理解したい→群論を理解したい→線形代数を身につける必要がある
のような流れで、かならずぶつかると思います。
(当たり前だろって? 線形代数をきちんと勉強したあなたはエラい!)
アホみたいな話ですが、非対称にマイナスが右上に出てくる理由についてなかなか腹落ちできません。
左回り90°、ぐるりと点を動かすとcos (θ+π/2) = –sin θ , sin (θ+π/2) = cos θ
で、非対称にマイナス記号が付くことなんかも、この問題と関係している。
(図形を描けば自明でも、不思議ではありませんか?これも昔から気持ち悪かった。)
暗記できても、なんだか気持ち悪いのはよくありません。
しばし思案して、スッキリとしたので備忘録です。
加法定理を使うとスッキリ理解できます。
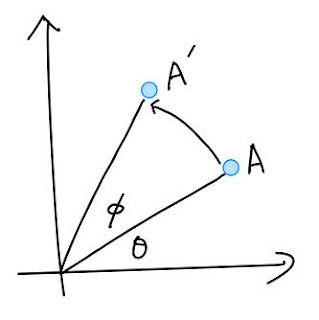
❏ 下の図で、単位円上にある点AをA'へと回転させるとしましょう。
A'の座標は、加法定理を使うと以下のように書けます。
(加法定理の図形的理解は、こちらの図が分かりやすい)
\begin{eqnarray}
A' = \begin{pmatrix}\cos(\theta+\phi)\\ \sin(\theta+\phi)\end{pmatrix}
\end{eqnarray}
加法定理より、
\begin{eqnarray} \cos(\theta+\phi) =\cos\theta\cos\phi–\sin\theta\sin\phi =\begin{pmatrix}\cos\phi&-\sin\phi\end{pmatrix}\begin{pmatrix}\cos\theta \\ \sin\theta \end{pmatrix} \end{eqnarray}
\begin{eqnarray} \sin(\theta+\phi) =\sin\theta\cos\phi+\cos\theta\sin\phi =\begin{pmatrix}\sin\phi&\cos\phi\end{pmatrix}\begin{pmatrix}\cos\theta \\ \sin\theta \end{pmatrix} \end{eqnarray}
(4)の変形では、項の順を変えています。
(3)と(4)をまとめると、
\begin{eqnarray} A' =\begin{pmatrix} \cos(\theta+\phi)\\ \sin(\theta+\phi)\end{pmatrix}\ &=& \begin{pmatrix} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{pmatrix} \begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix} &=& \boldsymbol{R}\begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix} \end{eqnarray}
となり、回転行列が得られました。
とゆうことで、回転行列右上の "–" は、cosの加法定理のマイナスと考えれば、忘れませんね。
sinの加法定理ではマイナスが入らないので、この非対称性が回転行列のマイナスの位置に影響を与えると考えれば、納得できるのではないでしょうか。
時計回りに回転させる場合は、θ – φ になるので、同様に求められます。
同様の流れで広島大山崎先生もまとめられているのを見つけました。
混乱しやすい、成分の回転と座標の回転についても力を入れて説明されています。
また、複素数の場合にまで拡張して、波動関数の計算まで扱われています。
❏ または、より本質的な説明は、以下のようになるでしょう。
回転行列は、合同変換(軸に対する反転等の操作を含む。群論で扱うような対称操作)を表現する行列の一つ。
合同変換を表すベクトルは、列ベクトル同士(と行ベクトル同士)が直交関係を持つ(つまり内積がゼロ)。また、それぞれの絶対値が1となる。
\begin{eqnarray} \mathbb{A}=\begin{pmatrix} p & q \\ r & s \end{pmatrix} \end{eqnarray} ただし、
\begin{eqnarray} \begin{pmatrix} p \\ r \end{pmatrix} \cdot \begin{pmatrix} q \\ s \end{pmatrix} =0 \\[10pt] p^{2}+r^{2}=1,\quad q^{2}+s^{2}=1 \end{eqnarray}
絶対値が1となる条件を用いると、それぞれの列ベクトルはsin, cosの2乗の和が1となることを用いて書き変えられます。
\begin{eqnarray} \mathbb{A}=\begin{pmatrix} \cos \phi & \cos \alpha \\ \sin \phi & \sin \alpha \end{pmatrix} \end{eqnarray}
内積が0になる条件を利用すると、
\begin{eqnarray} \cos \phi\cos \alpha + \sin \phi\sin \alpha =\cos (\phi-\alpha) = 0 \end{eqnarray}
最初の説明と同じ関係式がでてきました。ここで、cos が0になるということで、以下の式が立ちます。
\begin{eqnarray} \phi–\alpha = \dfrac {\pi }{2}+n\pi \end{eqnarray}
nが1の場合を考えると、
\begin{eqnarray} \alpha = \phi– \dfrac {3}{2}\pi\\ \end{eqnarray} \begin{eqnarray} \cos \alpha = \cos (\phi– \dfrac {3}{2}\pi)= –\sin\phi\\ \sin \alpha = \sin (\phi– \dfrac {3}{2}\pi)= \cos\phi\\[10pt] \mathbb{A}=\begin{pmatrix} \cos \phi & –\sin \phi \\ \sin \phi & \cos \phi \end{pmatrix} \end{eqnarray}
以上のように、回転行列と同じ形の行列が出て来ました。
まとめると、回転という操作は、ベクトルの絶対値等の性質を変えないまま、移動だけさせる変換(合同変換)の一つです。
合同変換を表す行列となるための厳しい制約(式7と8)を満たすものの一つが回転行列であり、内積を0にするためには、どこかに一つマイナスが入っている必要があるということです。これが非対称性の紀元と考えればよいでしょうか?
ちなみに、nを1としてときましたが、nが奇数でも同じ式が、
nを偶数として解くと、もう一つの行列が得られます。
\begin{eqnarray} \mathbb{A'}=\begin{pmatrix} \cos \phi & \sin \phi \\ \sin \phi & -\cos \phi \end{pmatrix} \end{eqnarray}
この行列A'は、軸に対する対称操作を示す行列シグマを使って、Aへと変換することができます。 \begin{eqnarray} \mathbb{A'}=\mathbb{A}\mathbb{\sigma}\\ \end{eqnarray}
\begin{eqnarray} \begin{pmatrix} \cos \phi & \sin \phi \\ \sin \phi & -\cos \phi \end{pmatrix}=\begin{pmatrix} \cos \phi & –\sin \phi \\ \sin \phi & \cos \phi \end{pmatrix}\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \end{eqnarray}
合同変換を表現する行列は、AとA'ですべてです。(さらにA'を掛けるという操作は、回転させてから鏡映させる、という群論ではおなじみの操作に対応していることもわかりますね。)
龍谷大池田先生の線形代数の資料を参考にさせて頂きました。
https://www.math.ryukoku.ac.jp/~tsutomu/LA1/09/lecture0905.pdf
❏ 複素平面でφだけ点を回転するときは、cosφ + i sinφ を掛け算することを思い出すと、他の見方もできます。
複素数ではiと書かれる数も、行列を使うと1と-1で表現することができます。虚数単位を表す二次正方行列を I と呼びます。
(I の二乗は –E になりますね!)
\begin{eqnarray} \boldsymbol{ I }= \begin{pmatrix}0&-1\\1&0\end{pmatrix} \end{eqnarray}
このIを実数の単位行列であるE と一緒に使うと、R は以下のようになります。
\begin{eqnarray} \boldsymbol{ R } = \cos\phi\begin{pmatrix}1&0\\0&1\end{pmatrix}+\sin\phi\begin{pmatrix}0&-1\\1&0\end{pmatrix} =\cos\phi\boldsymbol{ E }+ \sin\phi\boldsymbol{ I } \\ \end{eqnarray}
さもありなんという感じでしょうか。マイナスは右上にありますよね。ここの証明でも、同様に加法定理が使われます。当たり前ですが、根は同じですね。
これだけ頭にいれると、気持ちよく回転させられます!
線形代数を触っていると出てくる回転行列R、分かったようでわからない。
スペクトルを理解したい→群論を理解したい→線形代数を身につける必要がある
のような流れで、かならずぶつかると思います。
(当たり前だろって? 線形代数をきちんと勉強したあなたはエラい!)
アホみたいな話ですが、非対称にマイナスが右上に出てくる理由についてなかなか腹落ちできません。
左回り90°、ぐるりと点を動かすとcos (θ+π/2) = –sin θ , sin (θ+π/2) = cos θ
で、非対称にマイナス記号が付くことなんかも、この問題と関係している。
(図形を描けば自明でも、不思議ではありませんか?これも昔から気持ち悪かった。)
暗記できても、なんだか気持ち悪いのはよくありません。
しばし思案して、スッキリとしたので備忘録です。
加法定理を使うとスッキリ理解できます。
❏ 下の図で、単位円上にある点AをA'へと回転させるとしましょう。
A'の座標は、加法定理を使うと以下のように書けます。
(加法定理の図形的理解は、こちらの図が分かりやすい)
\begin{eqnarray}
A' = \begin{pmatrix}\cos(\theta+\phi)\\ \sin(\theta+\phi)\end{pmatrix}
\end{eqnarray}
加法定理より、
\begin{eqnarray} \cos(\theta+\phi) =\cos\theta\cos\phi–\sin\theta\sin\phi =\begin{pmatrix}\cos\phi&-\sin\phi\end{pmatrix}\begin{pmatrix}\cos\theta \\ \sin\theta \end{pmatrix} \end{eqnarray}
\begin{eqnarray} \sin(\theta+\phi) =\sin\theta\cos\phi+\cos\theta\sin\phi =\begin{pmatrix}\sin\phi&\cos\phi\end{pmatrix}\begin{pmatrix}\cos\theta \\ \sin\theta \end{pmatrix} \end{eqnarray}
(4)の変形では、項の順を変えています。
(3)と(4)をまとめると、
\begin{eqnarray} A' =\begin{pmatrix} \cos(\theta+\phi)\\ \sin(\theta+\phi)\end{pmatrix}\ &=& \begin{pmatrix} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{pmatrix} \begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix} &=& \boldsymbol{R}\begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix} \end{eqnarray}
となり、回転行列が得られました。
とゆうことで、回転行列右上の "–" は、cosの加法定理のマイナスと考えれば、忘れませんね。
sinの加法定理ではマイナスが入らないので、この非対称性が回転行列のマイナスの位置に影響を与えると考えれば、納得できるのではないでしょうか。
時計回りに回転させる場合は、θ – φ になるので、同様に求められます。
同様の流れで広島大山崎先生もまとめられているのを見つけました。
混乱しやすい、成分の回転と座標の回転についても力を入れて説明されています。
また、複素数の場合にまで拡張して、波動関数の計算まで扱われています。
❏ または、より本質的な説明は、以下のようになるでしょう。
回転行列は、合同変換(軸に対する反転等の操作を含む。群論で扱うような対称操作)を表現する行列の一つ。
合同変換を表すベクトルは、列ベクトル同士(と行ベクトル同士)が直交関係を持つ(つまり内積がゼロ)。また、それぞれの絶対値が1となる。
\begin{eqnarray} \mathbb{A}=\begin{pmatrix} p & q \\ r & s \end{pmatrix} \end{eqnarray} ただし、
\begin{eqnarray} \begin{pmatrix} p \\ r \end{pmatrix} \cdot \begin{pmatrix} q \\ s \end{pmatrix} =0 \\[10pt] p^{2}+r^{2}=1,\quad q^{2}+s^{2}=1 \end{eqnarray}
絶対値が1となる条件を用いると、それぞれの列ベクトルはsin, cosの2乗の和が1となることを用いて書き変えられます。
\begin{eqnarray} \mathbb{A}=\begin{pmatrix} \cos \phi & \cos \alpha \\ \sin \phi & \sin \alpha \end{pmatrix} \end{eqnarray}
内積が0になる条件を利用すると、
\begin{eqnarray} \cos \phi\cos \alpha + \sin \phi\sin \alpha =\cos (\phi-\alpha) = 0 \end{eqnarray}
最初の説明と同じ関係式がでてきました。ここで、cos が0になるということで、以下の式が立ちます。
\begin{eqnarray} \phi–\alpha = \dfrac {\pi }{2}+n\pi \end{eqnarray}
nが1の場合を考えると、
\begin{eqnarray} \alpha = \phi– \dfrac {3}{2}\pi\\ \end{eqnarray} \begin{eqnarray} \cos \alpha = \cos (\phi– \dfrac {3}{2}\pi)= –\sin\phi\\ \sin \alpha = \sin (\phi– \dfrac {3}{2}\pi)= \cos\phi\\[10pt] \mathbb{A}=\begin{pmatrix} \cos \phi & –\sin \phi \\ \sin \phi & \cos \phi \end{pmatrix} \end{eqnarray}
以上のように、回転行列と同じ形の行列が出て来ました。
まとめると、回転という操作は、ベクトルの絶対値等の性質を変えないまま、移動だけさせる変換(合同変換)の一つです。
合同変換を表す行列となるための厳しい制約(式7と8)を満たすものの一つが回転行列であり、内積を0にするためには、どこかに一つマイナスが入っている必要があるということです。これが非対称性の紀元と考えればよいでしょうか?
ちなみに、nを1としてときましたが、nが奇数でも同じ式が、
nを偶数として解くと、もう一つの行列が得られます。
\begin{eqnarray} \mathbb{A'}=\begin{pmatrix} \cos \phi & \sin \phi \\ \sin \phi & -\cos \phi \end{pmatrix} \end{eqnarray}
この行列A'は、軸に対する対称操作を示す行列シグマを使って、Aへと変換することができます。 \begin{eqnarray} \mathbb{A'}=\mathbb{A}\mathbb{\sigma}\\ \end{eqnarray}
\begin{eqnarray} \begin{pmatrix} \cos \phi & \sin \phi \\ \sin \phi & -\cos \phi \end{pmatrix}=\begin{pmatrix} \cos \phi & –\sin \phi \\ \sin \phi & \cos \phi \end{pmatrix}\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \end{eqnarray}
合同変換を表現する行列は、AとA'ですべてです。(さらにA'を掛けるという操作は、回転させてから鏡映させる、という群論ではおなじみの操作に対応していることもわかりますね。)
龍谷大池田先生の線形代数の資料を参考にさせて頂きました。
https://www.math.ryukoku.ac.jp/~tsutomu/LA1/09/lecture0905.pdf
❏ 複素平面でφだけ点を回転するときは、cosφ + i sinφ を掛け算することを思い出すと、他の見方もできます。
複素数ではiと書かれる数も、行列を使うと1と-1で表現することができます。虚数単位を表す二次正方行列を I と呼びます。
(I の二乗は –E になりますね!)
\begin{eqnarray} \boldsymbol{ I }= \begin{pmatrix}0&-1\\1&0\end{pmatrix} \end{eqnarray}
このIを実数の単位行列であるE と一緒に使うと、R は以下のようになります。
\begin{eqnarray} \boldsymbol{ R } = \cos\phi\begin{pmatrix}1&0\\0&1\end{pmatrix}+\sin\phi\begin{pmatrix}0&-1\\1&0\end{pmatrix} =\cos\phi\boldsymbol{ E }+ \sin\phi\boldsymbol{ I } \\ \end{eqnarray}
さもありなんという感じでしょうか。マイナスは右上にありますよね。ここの証明でも、同様に加法定理が使われます。当たり前ですが、根は同じですね。
これだけ頭にいれると、気持ちよく回転させられます!
コメント
コメントを投稿