量子化学の落とし穴（１）電子の波長？と光の運動量？
量子化学を勉強していて、引っかかってしまうとなかなか抜け出せないポイントというのがあると思います。昔の自分に向けて、Schödinger 方程式に入る前の下ごしらえ部分を記しました。
具体的には、「光の運動量」という概念が、どういう理論や実験で担保されているのかというところだ。光には質量がないという話が一般的だが・・・？
＿＿＿＿＿＿
光（電磁波）のエネルギー（E）は、プランク定数（h）を単位として振動数（ν）に比例する。
また、光の振動数を波長（λ）と掛け合わせると、光速（c）となる。
この関係には、プランク•アインシュタインの関係（Plank–Einstein relation）という量子論の巨頭の名前が冠されている。
\begin{align} E = h\nu = h\frac{c}{\lambda} \end{align}
光はエネルギーを持っていることについては、違和感なく受け入れられているとおもいます。光は運動量も持っていると言われたら？
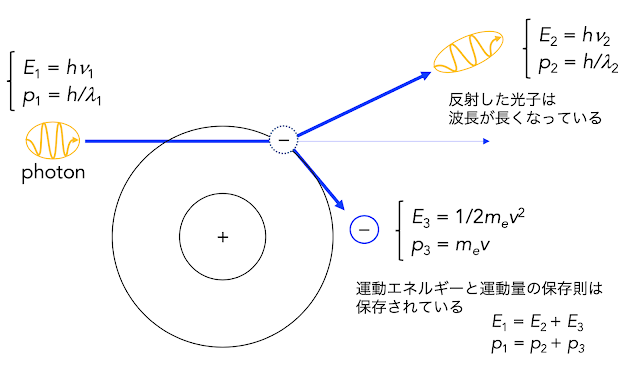
コンプトンは、様々な物質にX線を当て、その反射を観察しているときに、反射に伴いX線の波長が長くなっている事を見つけた。この実験事実は光が粒子として電子にぶつかって、方向が変わっていると解釈すると納得できる（粒子性の提唱自体は、アインシュタインの功績。cf. 光電効果）。粒子同士の衝突と考えれば、光にも「運動量」という量を考えてやっても良いのではないか[下図]。（すっ飛ばされた電子のほうは、後に観測された。）
図. コンプトン効果の模式図. 電子が原子から飛び出すのは、光子によって運動量（および運動エネルギー）を与えられたためである。電子が持つX,Y方向の運動量は、光子の運動量を (h/λ) として、そのX,Y成分を考えてやれば辻褄が合う。高校のときに、こんな問題をやったな。。
運動量とは p = mv で表現されるあれである。量子化学では、やたらと運動量がでてくる。
光の速度は「c」として一定、さらに光は質量を持たないと、学校では教えられたような・・・？ このあたりで化学系（私のことです）は、ツボってしまいます。
確かに、ニュートン力学の範囲では上記の形式で十分ですが、光速に近い領域では不十分で、式（２）のような形式で、粒子の速度、運動量、エネルギーは関係づけられます。
\begin{align} m^{2}c^{4}+ p^{2}c^{4} = E^{2} \end{align}
いわゆる、相対性理論というやつです。みんな（名前だけは）大好きなやつです。
あれ？よく見る E = mc^2 とちゃうやんけ？と、お思いでしょう。
上の式の p を mv としてやると、
\begin{align} E=mc\sqrt {c^{2}+v^{2}} \end{align}
となって、物体の速度 v が c よりとても遅いときには無視（近似して０）していいよ、ということです。じゃあ、m が 0 の光子は？というと、E = pc^2 となります。
（沖縄の前野先生の解説 ）
ほんまに運動量あるんかい、という気持ちにもなりますが、光が生む圧力「光圧」を利用した太陽帆という装置があります。
そういえば、高校の時の物理教師のオッサンもそんな話をしていたなぁ（遠い目）。
ド・ブロイは、この辺の話に刺激を受けて、光が運動量を持っているのであれば、電子を始めとする粒子に波長を定義してやってもええやんけ！と考えた。（そしてD論にまとめた。スゴい）
冒頭の式と合わせると、
\begin{align} E=pc= h\frac{c}{\lambda} \Rightarrow \lambda=\frac{h}{p} \end{align}
となり、電子の「波長」は、プランク定数と運動量で定義できることになる。
電子の持つ波動性は、日立にいらっしゃった外村博士のきれいな実験でも確認されました。（日立の外村先生の業績解説ページ ）
とりあえず、光は質量を持たないけれど運動量を定義できるんだな、と納得していただけたかな、と思います。それでもまだ古典的なエネルギーと運動量の議論と、波をベースとした議論の間のギャップに疑問がある方は、広島大学山崎先生のモノローグによいものがあるので、目を通されると幸せになれるかも知れません。
むちゃくちゃ要約すると、物質波について考えるときは、波の位相速度と「群速度」について分けて考えましょうという話です。我々の身の回りの現象を支配する「力学」は、粒子そのものではなく、粒子が集まった物体について考えます。このような条件では、物質波が束ねられた、波の束を考えてやらないといけません。位相がずれたサイン波を足し合わせると「うねり」を生じますが、この「うねり」の速度のことを群速度と呼びます。
このへんにしておきましょう。エンジョイ、量子化学！
[2020/3/9] 誤植を訂正しました。E = pc → pc^2
具体的には、「光の運動量」という概念が、どういう理論や実験で担保されているのかというところだ。光には質量がないという話が一般的だが・・・？
＿＿＿＿＿＿
光（電磁波）のエネルギー（E）は、プランク定数（h）を単位として振動数（ν）に比例する。
また、光の振動数を波長（λ）と掛け合わせると、光速（c）となる。
この関係には、プランク•アインシュタインの関係（Plank–Einstein relation）という量子論の巨頭の名前が冠されている。
\begin{align} E = h\nu = h\frac{c}{\lambda} \end{align}
光はエネルギーを持っていることについては、違和感なく受け入れられているとおもいます。光は運動量も持っていると言われたら？
コンプトンは、様々な物質にX線を当て、その反射を観察しているときに、反射に伴いX線の波長が長くなっている事を見つけた。この実験事実は光が粒子として電子にぶつかって、方向が変わっていると解釈すると納得できる（粒子性の提唱自体は、アインシュタインの功績。cf. 光電効果）。粒子同士の衝突と考えれば、光にも「運動量」という量を考えてやっても良いのではないか[下図]。（すっ飛ばされた電子のほうは、後に観測された。）
運動量とは p = mv で表現されるあれである。量子化学では、やたらと運動量がでてくる。
光の速度は「c」として一定、さらに光は質量を持たないと、学校では教えられたような・・・？ このあたりで化学系（私のことです）は、ツボってしまいます。
確かに、ニュートン力学の範囲では上記の形式で十分ですが、光速に近い領域では不十分で、式（２）のような形式で、粒子の速度、運動量、エネルギーは関係づけられます。
\begin{align} m^{2}c^{4}+ p^{2}c^{4} = E^{2} \end{align}
いわゆる、相対性理論というやつです。みんな（名前だけは）大好きなやつです。
あれ？よく見る E = mc^2 とちゃうやんけ？と、お思いでしょう。
上の式の p を mv としてやると、
\begin{align} E=mc\sqrt {c^{2}+v^{2}} \end{align}
となって、物体の速度 v が c よりとても遅いときには無視（近似して０）していいよ、ということです。じゃあ、m が 0 の光子は？というと、E = pc^2 となります。
（沖縄の前野先生の解説 ）
ほんまに運動量あるんかい、という気持ちにもなりますが、光が生む圧力「光圧」を利用した太陽帆という装置があります。
そういえば、高校の時の物理教師のオッサンもそんな話をしていたなぁ（遠い目）。
ド・ブロイは、この辺の話に刺激を受けて、光が運動量を持っているのであれば、電子を始めとする粒子に波長を定義してやってもええやんけ！と考えた。（そしてD論にまとめた。スゴい）
冒頭の式と合わせると、
\begin{align} E=pc= h\frac{c}{\lambda} \Rightarrow \lambda=\frac{h}{p} \end{align}
となり、電子の「波長」は、プランク定数と運動量で定義できることになる。
電子の持つ波動性は、日立にいらっしゃった外村博士のきれいな実験でも確認されました。（日立の外村先生の業績解説ページ ）
とりあえず、光は質量を持たないけれど運動量を定義できるんだな、と納得していただけたかな、と思います。それでもまだ古典的なエネルギーと運動量の議論と、波をベースとした議論の間のギャップに疑問がある方は、広島大学山崎先生のモノローグによいものがあるので、目を通されると幸せになれるかも知れません。
むちゃくちゃ要約すると、物質波について考えるときは、波の位相速度と「群速度」について分けて考えましょうという話です。我々の身の回りの現象を支配する「力学」は、粒子そのものではなく、粒子が集まった物体について考えます。このような条件では、物質波が束ねられた、波の束を考えてやらないといけません。位相がずれたサイン波を足し合わせると「うねり」を生じますが、この「うねり」の速度のことを群速度と呼びます。
このへんにしておきましょう。エンジョイ、量子化学！
[2020/3/9] 誤植を訂正しました。E = pc → pc^2
コメント
コメントを投稿